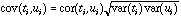
Co-inertia analysis of amino-acid physico-chemical properties and protein composition with the ADE package
Thioulouse, J.* and Lobry, J.R.
Laboratoire de Biométrie, Génétique et Biologie des Populations
URA CNRA 243
Université Lyon 1
69622 Villeurbanne CEDEX
FRANCE
e-mail address: Jean.Thioulouse@biomserv.univ-lyon1.fr
Running head: Co-inertia analysis with the ADE package
Keywords: Co-inertia analysis, Macintosh, ADE, amino-acids, proteins
* To whom reprint requests should be sent.
Abstract
A multivariate analysis method called co-inertia analysis was used to determine the main relationships between two data tables having identical rows. This method is available in the ADE multivariate analysis package for Macintosh micro-computers. It was applied to two data sets, one containing the amino-acid composition of 999 E. coli proteins, and the other the values of 402 physico-chemical properties for the 20 natural amino-acids. There were strong relationships between amino-acid physico-chemical properties and the composition of proteins. The first common factor was hydrophobicity; it is linked to the biological environment of proteins, either in the cytoplasm (or outside the cell), or in the non- polar environment of the phospholipid bilayer of biological membranes. The second factor linked the expressivity of protein genes and the propensity of amino-acids to form alpha helix / beta sheets. The third factor showed that heavy, aromatic amino-acids tend to be avoided, except when they are needed for structural or functional reasons. These results are discussed in terms of selective pressure acting on amino-acid composition of proteins.
Introduction
Standard multivariate analysis tools such as principal component analysis (PCA) or correspondence analysis (CA) are very useful for summarizing a single set of numerical data as simple interpretable factors. These multivariate analysis methods are available on numerous commercial or freeware packages. The increase in the number of molecular databases freely available on the Internet raises the question of how to take advantage of information from different data sets. Combining such data requires sophisticated multivariate analysis tools which can analyse more than one data set simultaneously. These methods are less common than the usual PCA and CA. This paper illustrates the results that can be obtained by crossing two data sets with the ADE package (Analysis of Environmental Data, Thioulouse et al., 1995), in which these methods are implemented. We have attempted to cross information on amino-acid physico-chemical properties and protein composition.
Multivariate analysis revealed that the between-species variability of protein composition is low (Grantham et al., 1980), at least when compared with the between-species codon usage variability. Three main interpretable factors underly the variability in the composition of E. coli proteins (Lobry and Gautier, 1994). These factors are, in decreasing order of importance, protein hydrophobicity , the expressivity level of their corresponding genes, and the aromaticity of the proteins themselves.
The situation for amino-acids physico-chemical properties is more confused because the main factors are not readily identified (Sneath, 1966). The datasets analysed and the methods used also differed from author to author. From a dataset of 134 qualitative amino-acid properties, Sneath (1966) tentatively identified the first three factors as aliphaticity, hydrogenation, and aromaticity. Sjöström and Wold (1985) identified the first three factors from a dataset of 20 quantitative properties as being lipophilicity, side chain bulk, and electronic properties. Kidera et al. (1985) found that 10 orthogonal factors were sufficient to represent almost all the variability of 188 published indices, showing that these indices are very redundant. Nakai et al. (1988), working with 222 amino-acid indices and a hierarchical cluster analysis, found four main clusters of amino-acid features, alpha and turn propensities, beta propensities, hydrophobicity, and other physico-chemical properties.
This paper investigates the amino-acid composition of proteins and the physico-chemical properties of amino-acids in parallel using the ADE package to perform a co-inertia analysis of two datasets. The aim was not to predict protein composition (see Wold et al. (1987) and Hellberg et al. (1986) for examples of predicting protein biological activity). The objective was to find the major relationships between the physico-chemical properties of amino-acids and protein composition.
System and methods
Algorithm
Co-inertia (or co-structure) analysis (Chessel and Mercier, 1993; Dolédec and Chessel, 1994) is a "data coupling" approach to multivariate analysis. It allows the simultaneous analysis of two data sets. In agronomy and ecology, these data sets are often an environmental table (physico-chemical variables) and a floro-fauna table (species abundance) measured at the same sampling points. Many methods have been suggested for analysing such data (see a review by Chessel and Mercier,1993), one of the simplest from the theoretical point of view is co-inertia analysis. Tucker (1958) described such an analysis under the name of inter-battery factor analysis in the case of two PCA tables. The method has also been proposed as an alternative to canonical analysis for environmental data (Gittins, 1985), and generalized to any type of table (quantitative, qualitative, or contingency) by Mercier (1991). It is also similar to the canonical correspondence analysis (CCA) of ter Braak (1986) and the partial least square regression method (PLS) used by Wold et al., 1987; Hellberg et al., 1986; Höskuldsson, 1988.
Co-inertia analysis was used on to the two data sets described in the Data Sets. The data were arranged in two tables, one with 20 rows (amino-acids) and 402 columns (physico-chemical and biological properties), and the second with 20 rows and 999 columns (E. coli proteins).
The geometrical interpretation of co-inertia analysis is simple. Standard methods (PCA, CA, and multiple correspondence analysis (MCA)) summarize a table by searching orthogonal axes on which the projection of the sampling points (rows of the table) have the highest possible variance. This characteristic ensures that the associated graphs (factor planes) provide good representations of the initial data. Canonical correlation analysis searches successive pairs of axes (ti and ui, one for each table) with a maximum correlation to extract information common to both tables. By maximizing the covariance instead of the correlation, co-inertia analysis maximizes the product of the correlation by the variances projected on axes ti and ui :
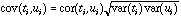
This ensures that these axes will correlate well together like canonical analysis axes, and also real significance (i.e., a high percentage of explained variance) with respect to each table, like PCA and CA axes. Another important feature of co-inertia analysis is that, like PLS, it can be used when the number of variables is greater that the number of observations. This is obviously unacceptable in standard methods like multiple regression, canonical analysis, or canonical correspondence analysis.
It can also be shown that co-inertia analysis is the analysis of a crossed
table having a simple meaning. An element of this crossed table (999 rows and
402 columns) is the mean value of a physico-chemical property weighted by the
frequency of a specific amino-acid in the protein. If
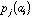is the value of physico-chemical property j for amino-acid i, and
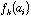the frequency of amino-acid i in protein k, then the generic term
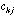in the crossed table will be:
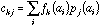
See Chessel and Mercier (1993) or Dolédec and Chessel (1994) for a more detailed explanation of the theory of co-inertia analysis.
Two sets of factor scores were obtained for the amino-acids (scores of the rows of both tables). They were used to draw the standard factor maps, and to compare them to the PCA and CA scores. We also obtained factor scores for the 402 properties and for the 999 proteins (scores of the rows and columns of the crossed table).
Lastly, a permutation test was used to check the significance of the co-structure. This method consists in repeated random permutations of the rows of the tables (i.e., of amino-acids), followed by re-computation of the total variability (also called inertia). Comparing the inertia obtained in the normal analysis with the inertias obtained after permutations provides an estimation of the probability of finding the observed situation in the absence of relationships between amino-acid properties and protein composition.
Implementation
Computations and graphical displays were obtained using the ADE package (Chessel and Dolédec, 1993; Thioulouse et al., 1995). All computations were performed with ADE version 4.0 on an Apple PowerMacintosh 8100/80 with 16 megabytes RAM (random access memory). The data type for floating point variables was long double (10 bytes). Computation times were 10 seconds for the PCA, 15 seconds for the CA, and 56 minutes for the co-inertia analysis using MC680x0 microprocessor emulation. Using a native compiler (generating PowerPC601 microprocessor code) reduced the computation time 10-fold (about 1 second for PCA and CA, 5 minutes for co-inertia analysis). Improvements in the algorithm should provide computation times for co-inertia analysis comparable to those for PCA and CA: the matrix from which eigenvalues and eigenvectors are computed will be of dimension min(n, p, q), with n = number of observations, p = number of variables in the first table, q = number of variables in the second table (instead of min(p, q) as is now the case).
ADE 4.0 is made up of a series of small independent modules written in ANSI C. These modules share the same simple user interface, and the computation code is isolated from the user interface code. The programming system allows the programmer to avoid implementing the user interface of the module he is writing: all the user interface details are automatically handled by a library of C functions. The modules can be used independently of each other and launched directly from the Macintosh Finder (stand-alone use), or they can be used through a HyperCard interface. The user can click to set the parameters of an analysis, and use the standard Macintosh dialogue windows (Figure 1). The latest version of ADE can be found at the following URL: ftp://biom3.univ- lyon1.fr/pub/mac/ADE.
Data Sets
The first data table used described the amino-acid composition of a sample of proteins from E. coli. The second contained various amino-acid properties. Both are readily available on the Internet.
The protein data set contains the absolute amino-acid frequencies of 999 protein sequences encoded by genes on the E. coli chromosome. Plasmid-encoded genes, partial sequences, poorly documented open reading frames, protein of less than 100 amino-acids, and seleno-cysteine containing proteins were all discarded. The N-terminal methionine was not removed and post-translational modifications were not taken into account. The data set contained only a single protein copy per locus to avoid overweighting due to sequence redundancy or DNA polymorphism. This data set represents about 25 % of the estimated total number of chromosome-encoded proteins in E. coli. It was extracted from the ECOSEQ6 collection (Rudd, 1993). This data set is available and described at the following URL: ftp://biom3.univ- lyon1.fr/pub/datasets/CABIOS95. This data set is the same as the one analysed with CA by Lobry and Gautier (1994).
The amino-acid data set is a compilation of 402 published physicochemical and biochemical properties of the 20 amino-acids occuring naturally in proteins (Nakai et al., 1988). This data set is available and described at the URL : ftp://ftp.genome.ad.jp/pub/db/genomenet/aaindex. Two subset of this dataset have been analysed previously (Kidera et al., 1985, Nakai et al., 1988).
Results
Co-structure significance
Figure 2 shows that the total variability of the dataset was far higher than the variability computed after randomization of the rows (i.e., of amino-acids). Thus the co-structure between the amino-acid composition of proteins and the properties of these amnino-acids is highly significant.
Selection of factors
Figure 3 shows that three main factors explain the total variability of the co-inertia analysis. They account for 52%, 16% and 13% of the explained variance, respectively. These 3 factors therefore account for 81% of the total variability of the co-intertia analysis, and are a good summary of the intial co-structure between protein composition and amino-acid properties.
Factor one (F1)
The 20 most important proteins for defining F1 are listed in Table 1. Those with a negative F1 score were all integral membrane proteins. They are all involved in membrane related functions, such as transport through the membrane (e.g., BtuC for vitamin B12 transport and PotB for putrescine and spermidine transport, anchoring dehydrogenases to the cytoplasmic membranes (e.g., SdhD for succinate dehydrogenase complex, FrdD for the fumarate reductase complex), cytoplasmic membrane redox reactions (e.g., CyoD, the cytochrome o ubiquinol oxidase). Figure 4 shows that these proteins are enriched in hydrophobic amino-acids (Ile, Leu, Met, Phe, Trp) and tends to have fewer hydrophilic amino-acids (Arg, Asp, Gln, Glu, Lys). The proteins with a positive F1 score were more heterogenous, including proteins enriched in hydrophilic amino-acids (the histone-like DNA binding proteins Hns, and the single-strand binding protein Ssb, which are very rich in positively charged residues in order to bind to the negatively charged phosphate-sugar backbone of DNA). The distribution of the F1 score was bimodal, showing that there were great differences between integral membrane proteins and the others in terms of their amino-acid frequencies. Thus, the most important factor underlying the differences in the amino-acid composition of proteins is their sub-cellular location. Proteins buried in the membrane have few hydrophilic amino-acids.
The 20 most important amino-acid indices for defining F1 are listed in Table 2. Those with a positive F1 score are all clearly correlated with a hydrophilic scale, with higher values for hydrophilic amino-acids. The polarity scale, as defined by Grantham (1974), is positively correlated with the hydrophilic nature of amino-acids since water is a polar solvent; and the transfer free energy to a lipophilic phase (von Heijne and Blomger, 1979) is greater for hydrophilic amino-acids. The fact that the principal property value z1 (Wold et al., 1987) is on the list of the most important amino-acid indices demonstrates the consistency of our results with previous multivariate analyses. The amino-acid indices with a negative F1 score were positively correlated on hydrophobic scale, such as the Kyte and Doolittle (1982) hydropathy index, which assigns higher values to hydrophobic amino-acids (fig. 5). The normalized composition of membrane proteins (Nakashima et al., 1990) also belongs to this group, because the membrane proteins contain more hydrophobic amino-acids than hydrophilic ones. Thus F1 reflects the hydrophilic character of amino-acids, with the hydrophobic and hydrophilic scales negatively correlated.
Factor two (F2)
The 20 most important proteins for defining F2 are listed in Table 1. Proteins with a high F2 score were often outer membrane proteins, like the porins OmpC and OmpF, the vitamin B12 receptor protein BtuB, the protease VII OmpT, and the long-chain fatty acid receptor FadL. This was not, however, a general rule, since Ssb is a DNA-binding protein, TolB a periplasmic protein associated with the inner membrane, and FliC the subunit protein which polymerizes to form the filaments of bacterial flagella. The most striking feature of these proteins is that they all have high Gly and Pro contents (Figure 4), and less Glu and Leu, which suggests that these proteins have few alpha-helix domains. This is consistent with the X-ray cristallography study of OmpF, which showed that each subunit of the porin consists of a 16-stranded anti-parallel beta-barrel containing the hydrophilic pore. As the primary amino-acid sequence of OmpC is similar to that of OmpF, they probably have similar 3D-structures, with little alpha-helix, for OmpC. In contrast, proteins with a negative F2 score contain few Pro and Gly residues, which suggests that these proteins are rich in alpha-helix structures. TolA, a periplasmic protein associated with the inner membrane fits this picture; its domain II (62 % of total amino-acid) has been shown by circular dichroism studies to be predominantly alpha-helical in structure. The trp operon repressor TrpR, whose structure was determined by X-ray crystallography and NMR (nuclear magnetic resonance), also has a high helical content. Lastly, the phage shock-associated protein PspA has the heptad repeats characteristic of proteins that can form coiled-coil alpha-helices. Hence, F2 factor appears to be the alpha-helical content of proteins, which induces a variability in terms of alpha-helix breaker amino-acid composition.
The 20 most important amino-acid indices for defining F2 are listed in Table 2. Those with a positive value are all indices for the propensity of an amino-acid to be found in coils, turns or beta-sheets. In contrast, indices with a negative F2 indicate only the propensity of amino-acids to be found in an alpha-helix, with low values for Gly and Pro which are both known helix breakers, and also, to a lesser extent, for Asn, Ser and Thr. Ala, Gln, Glu, Leu, Lys, Met, Phe and Trp, which are all preferentially found in alpha-helices (Figure 5) have high scores. Hence, F2 reflects the spectrum between amino-acids that are mainly found in alpha-helices and amino-acids that are found mainly in other conformations.
Factor three (F3)
The 20 most important amino-acid indices for defining F3 are listed in Table 1. There is no special common feature for proteins with a positive F3 score, except that they all contain few aromatic amino-acids. Proteins with a negative F3 score are enriched in aromatic amino acids (e.g., cytochromes). F3 therefore represents a gradient of aromatic amino-acid content in proteins. This gradient was interpreted as a compromise between selective pressure, that tends to remove the expensive aromatic amino-acids, and structural or functional constraints which impose a minimum aromatic content, at least for some proteins. This structural constraint is illustrated by the correlation between aromatic amino-acids at positions i and i+4 in proteins (Klingler and Brutlag, 1994).
The 20 most important amino-acid indices that define F3 are listed in Table 2. Indices with a positive F3 score are correlated with the frequency of amino-acids in natural proteins, with low values for rare amino-acids like Trp and Cys. Indices with a negative F3 score are positively correlated with the molecular weight of amino-acids, for instance the aromaticity of amino-acids because aromatic amino-acids are also the heaviest amino-acids. Thus, F3 reflects the contrast between indices of amino-acid frequency in proteins and indices related to the size of amino-acids.
Discussion
The relationships between amino-acid physico-chemical properties and protein composition shown by the first three factors of co-inertia analysis must be interpreted in terms of biological and evolutionary constraints.
Factor 1
The overall hydrophobicity of proteins has been shown to be the major factor underlying variations in the amino-acid composition of E. coli proteins (Lobry and Gautier, 1994). Their hydrophobic character is also an important property discriminating between amino-acids (Sneath, 1966). The co-inertia analysis shows that this factor, hydrophobicity, is the most important factor underlying the variability of amino-acid composition of proteins and the properties of amino-acids. This can be interpreted in terms of protein environment. There are two very different environments for a protein, in a polar aquous environment (cytoplasm, periplasm, outside the cell), or the non-polar environment of the phospholipid bilayer of biological membranes. During the course of evolution, amino-acids were selected to enable proteins to colonize these two environments. There was a selective advantage in amnio-acids with a wide range of solubilities, so that proteins could be stable in both environments. This kind of centrifugal selection ensures that the hydrophobicity of present day amino-acids in proteins is a highly discriminating property, and is also a major characteristic of amino-acids.
Factor 2
The results of the co-inertia analysis are somewhat different from the results of analysing the two data sets separately. The second factor underlying variability in protein composition is the expressivity level (the extent to which the corresponding genes are expressed, see Gouy and Gautier, 1982). As the major tRNA concentations are not the same for all species, it is not surprising that this factor is not directly correlated with amino-acid indices, which are not specific of species. However, there may well be an indirect link via the helix-content of proteins: poorly expressed genes are often regulatory genes that interact with DNA via their alpha-helix structure. Conversely, the most active genes include those for the outer membrane proteins, which are rich in beta-sheet. Although this rule may have many exceptions, it could explain the coupling between the two analyses.
Factor 3
The results of the co-intertia analysis for the third axis are very similar to those obtained when the data sets are analyzed independently. A simple explanation for this is that the amino-acid content of a protein is subject to selective pressure because the cost, in terms of both energy and matter for the cell, is not the same for all amino-acids. It is not surprising that the cost of heavy and aromatic amino-acids is greater, so that they tend to occur less frequently.
Conclusion
Analysis of the co-structure of the two data sets helps to show how the variability of protein composition depends on amino-acid properties, and, conversely, how amino-acids properties vary with protein composition. The co-structure is in fact easier to interpret than the structure of each data set alone, because each factor is analysed from two points of view, and is contrained to explain both protein compositions and amino-acid properties. This works well because there is a strong co-structure between the two data sets. This strong co-structure arises because proteins are subject to selective pressure on their amino-acid compositions and the overall avantages or disadvantages for a given function are linked to the physico-chemical properties of their amino-acid content.
There is clearly a high local selective pressure on protein amino-acid contents, as indicated by the amino-acids involved in the catalytic site of an enzyme. But there are only a few of these crucial amino-acids (say 10), while the total number of amino-acids in a protein (may be 300). Hence, their contribution to the overall amino-acid composition of a protein is not likely to be important. The information used in the co-inertia analysis to describe proteins is only their overall amino-acid composition. As a result, the selective pressures demonstrated here act on the overall protein amino-acid composition, and the most important factor is the subcellular location of the proteins.
Acknowledgements
We thank D. Chessel and C. Gautier for helpful comments on a first draft of the manuscript.
References
Bachmann, B.J. (1990) Linkage map of Escherichia coli K-12, Edition 8. Microbiol. Rev., 54, 130-197.
Chessel, D. and Dolédec, S. (1993) ADE Version 3.7: - Program library for the Analysis of Environmental Data. Documentation, URA CNRS 1451, Université Lyon 1, 69622 Villeurbanne CEDEX, 1-750.
Chessel, D. and Mercier, P. (1993) Couplage de triplets statistiques et liaisons espèces-environnement. In: Lebreton J.D. and Asselain B. (eds), Biométrie et Environnement. Masson, Paris, pp. 15-44.
Dolédec, S. and Chessel, D. (1994) Co-inertia analysis: an alternative method for studying species-environment relationships. Freshwater Biology, 31, 277-294.
Gittins, R. (1985) Canonical analysis, a review with applications in ecology. Springer - Verlag, Berlin.
Gouy, M. and Gautier, C. (1982) Codon usage in bacteria: correlation with gene expressivity. Nucl. Acids Res., 22, 7055-7074.
Grantham, R. (1974) Amino-acid difference formula to help explain protein evolution. Science, 185, 862-864.
Grantham, R., Gautier, C. and Gouy, M. (1980) Codon frequencies in 119 individual genes confirm consistent choices of degenerated bases according to genome type. Nucl. Acids Res., 8, 1893-1912.
Hellberg, S., Sjöström, M. and Wold, S. (1986) The prediction of bradykinin potentiating potency of pentapeptides. An exemple of a peptide qunatitative structure-activity relationship. Acta Chemica Scandinavica, B40, 135-140.
Höskuldsson, A. (1988). PLS regression methods. Journal of Chemometrics, 2, 211-228.
Kidera, A., Konishi, Y., Oka, M., Ooi, T. and Scheraga, H.A. (1985) Statictical analysis of the physical properties of the 20 naturally occuring amino-acids. J. Prot. Chem., 4, 23-55.
Klingler, T.M. and Brutlag, D.L. (1994) Discovering structural correlations in alpha-helices. Prot. Sci., 3, 1847-1857.
Kyte, J. and Doolittle, R.F. (1982) A simple method for displaying the hydropathic character of a protein. J. Mol. Biol., 157, 105-132.
Lobry, J.R. and Gautier, C. (1994) Hydrophobicity, expressivity and aromaticity are the major trends of amino-acid usage in 999 Escherichia coli chromosome-encoded genes. Nucl. Acids Res., 22, 3174-3180.
Mercier, P. (1991) Etude des relations espèces-environnement et analyse de la co-structure d'un couple de tableaux. PhD Thesis, Université Lyon 1, Lyon, France.
Nakashima, H., Nishikawa, K. and Ooi, T. (1990) Distinct character in hydrophobicity of amino-acid composition of mitochondrial proteins. Proteins, 8, 173-178.
Nakai, K., Kidera, A. and Kanehisa, M. (1988) Cluster analysis of amino acid indices for prediction of protein structure and function. Prot. Eng., 2, 93-100.
Rudd, K.E. (1993) Maps, genes, sequences and computers: an Escherichia coli case study. ASM News, 7, 335-341.
Sjöström, M. and Wold, S. (1985) A multivariate study of the relationship between the genetic code and the physical-chemical properties of amino-acids.J. Mol. Evol., 22, 272-277.
Sneath, P.H.A. (1966) Relation between chemical structure and biological activity in peptides. J. Theoret. Biol., 12, 157-195.
ter Braak, C.J.F. (1986) Canonical correspondence analysis: a new eigenvector method for multivariate direct gradient analysis. Ecology, 67, 1167-1179.
Tucker, L.R. (1958) An inter-battery method of factor analysis. Psychometrika, 23, 111-136.
Thioulouse, J., Dolédec, S., Chessel, D. and Olivier, J.M. (1995). ADE software: multivariate analysis and graphical display of environmental data. In: Guariso G. and Rizzoli A. (Eds) Software par l'ambiente, Pàtron editore, Bologne, Italy (in press).
Von Heijne, G. and Blomberg, C. (1979) Trans-membrane translocation of proteins: the direct transfer model. Eur. J. Bioch., 97, 175-181.
Wold, S., Eriksson, L., Hellberg, S., Jonsson, J., Sjöström, M., Skagerberg, B. and Wikström, M. (1987) Principal property values for six non-natural amino-acids and their application to a structure-activity relationship for oxytocin peptide analogues. Can. J. Chem., 65, 1814-1820.
Table 1. Names (according to Bachman, 1990) of the 20 most important proteins for defining the first three factors of the co-inertia analysis. The first ten proteins have positive scores and the last ten negative ones.
F1 F2 F3
HflK TolB Tsf
Hns FadL OsmY
Ssb OmpT RbsB
RpsN FliC AceF
DksA BtuB FruA
MsyB OmpC FepD
HimA OmpF RplI
TolA RlpA MopA
PrfB Ssb FimA
DamX FimH TolA
SdhD PriC TdcR
MreD PspA HyaC
CyoD CelC SoxR
FrdD RplT FdnI
PotB Hns BarA
MvrC TrpR RfaS
DmsC TolA RfaK
AppB FliT CysX
BtuC MprA NarV
BicA FlhD CybB
Table 2. The 20 most important amino-acid indices for defining the first three factors of the co-intertia analysis. The first ten indices have positive scores and the last ten negative ones. They are referenced by their accession number in the data set, available at: ftp://ftp.genome. ad.jp/pub/db/genomenet/aaindex (see Nakai 1988).
F1 F2 F3
WOLS870101 ISOY800108 NAKH900102
VHEG790101 PALJ810106 NAKH900101
HOPT810101 LEWP710101 JOND920101
ROSM880101 ROBB760112 NAKH920102
WOEC730101 QIAN880124 RADA880103
ROSM880102 CRAJ730103 OOBM770105
MEIH800102 RACS820113 JUNJ780101
OOBM770101 PALJ810105 OOBM770104
PRAM900101 PALJ810116 JUKT750101
GRAR740102 RACS820109 DAYM780101
DESM900102 MAXF760101 FAUJ880106
NAKH900110 PALJ810109 MCMT640101
MEIH800103 TANS770101 FASG760101
BIOV880102 PALJ810102 LEVM760107
EISD860103 LEVM780101 CHAM820101
JANJ780102 PRAM900102 FAUJ880103
FAUJ830101 GEIM800104 CHOC750101
KYTJ820101 LEVM780104 SNEP660103
BIOV880101 ISOY800101 CHAM830106
ROSG850102 GEIM800101 LEVM760102
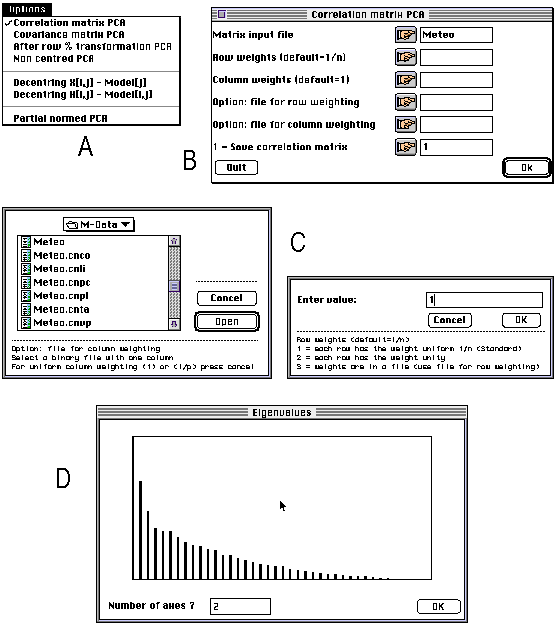
Figure 1. Screen shots of some windows of the principal component analysis module of ADE 4.0. All the modules have an "Options" menu enabling the user to choose between the available possibilities. Here, for example, it is possible to choose between PCA on correlation or on covariance matrix (A). According to the option selected by the user, a dialogue window is displayed, containing the parameters required for performing the computations (B). The user can click on the buttons of this window to set the values of these parameters through standard Macintosh dialogue windows (C). The values and a bar chart of eigenvalues is then diplayed and the user is asked to enter the number of axes on which factor scores will be computed (D).
*---------------------------------------------------------* | ADE THINK C(TM) library * CNRS-Lyon * JT/DC/MH | | CoInertia: Test w. one table fixed 06/12/94 21/46 | *---------------------------------------------------------* Warning: non uniform weighting. The results from permutations are valid only if the row weights come from the fixed table. ----- The fixed table is table 2: prot1r.fcta number of random matching: 1000 Observed: 3.421822 Histogramm: minimum = 1.880898, maximum = 3.421822 number of simulation X<Obs: 1000 (frequency: 1.000000) number of simulation X>=Obs: 0 (frequency: 0.000000) | |** |*********** |*************************** |************************************** |************************************************** |********************************************** |***************************************** |**************************** |**************** |************** |********* |***** |* |* | | | | *->|
Figure 2. Results of the permutation test. The test shows that the probability of obtaining a total variability equal to 3.42 (i.e., the inertia obtained in the co-inertia anlaysis) using the hypothesis of independence between amino-acid physico-chemical properties and protein composition is less than 0.001.
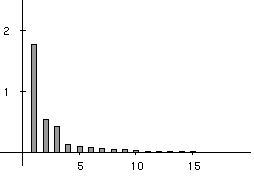
Figure 3. Eigenvalues bar chart of the co-inertia analysis. The first three eigenvalues are obviously greater than the following ones. Starting from the fourth eigenvalue, the values slowly decrease without any marked variations, showing that the rest of the structure can be discarded. These first three eigenvalues acounts for 81% of the total variability (52%, 16%, and 13% respectively).
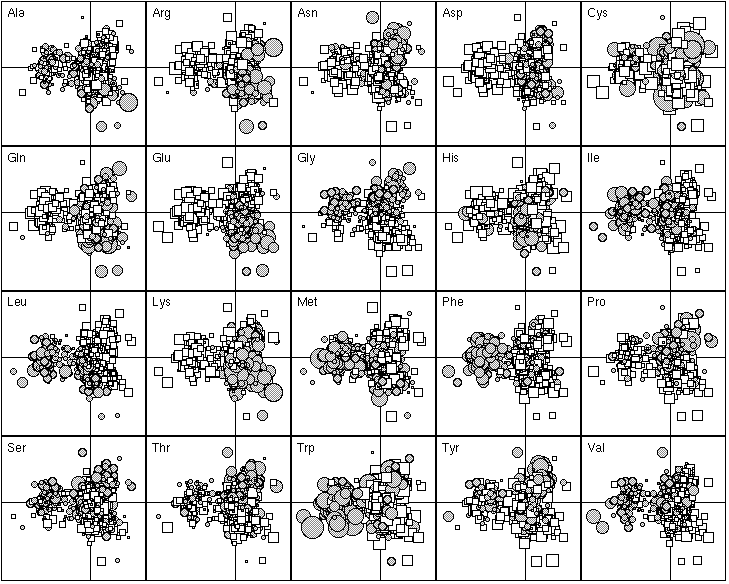
Figure 4. First factor map of the 999 proteins. This graph is a collection of 20 elementary graphs, all at the same scale, corresponding to the 20 amino-acids. Each elementary graph, shows the F1 x F2 factor map (F1 is on the x-axis and F2 on the y-axis), with, for each protein, a circle or a square whose size is proportional to the centered relative frequency of the corresponding amino-acid in the protein. Circles indicate positive values and squares negative ones. See text for interpretation.
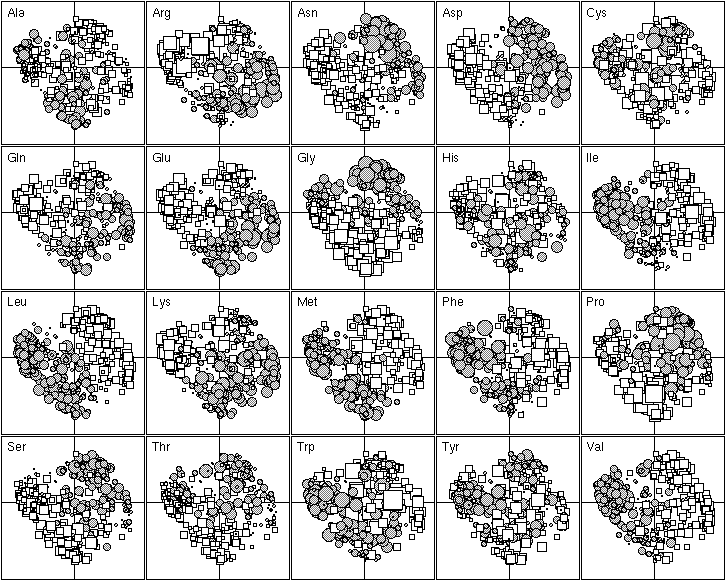
Figure 5. First factor map of the 402 amino-acid physico-chemical indices. Like figure 4, this graph is a collection of 20 elementary graphs, all at the same scale, corresponding to the 20 amino-acids. Each elementary graph shows the F1 x F2 factor map (F1 is on the x-axis and F2 on the y-axis), with, for each index, a circle or a square whose size is proportional to the standardized value of the index. Circles indicate positive values and squares negative ones. See text for interpretation.